FEM

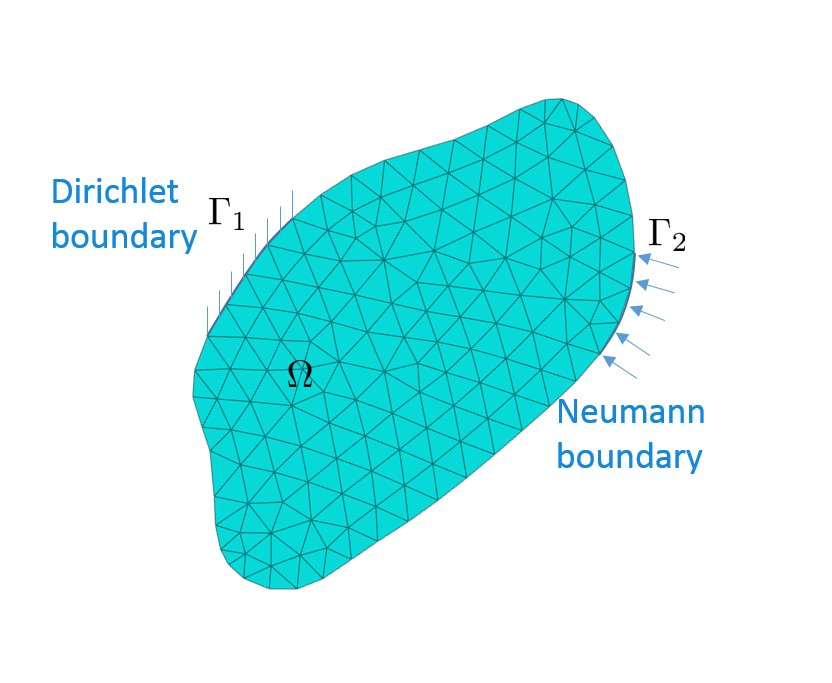
Let us consider an elastic deformable body $\Omega$. The discrete form of equilibrium equation should take the following form $\mathbf{K} \mathbf{u} = \mathbf{F}$, where $\mathbf{K}$ is the stiffness matrix, $\mathbf{F}$ is the vector of (external) load, and $\mathbf{u}$ is the vector of nodal displacements. For simplicity, we assume that $\Omega$ is a two dimensional rectangular … Read more

Strong formulation of the governing (partial differential equation) equation of steady-state transfer conduction $ \nabla \cdot \mathbf{\mathbf{k} \nabla T} + Q = 0 $, (1) in which $T$ is the temperature; $\mathbf{k} = diag(k_{xx}, k_{yy}, k_{zz})$ is the tensor of thermal conductivity; $Q$ is the heat sink/heat source. Boundary conditions are given by $T = … Read more

Shape functions (defined in natural coordinates) $N_{1} = \frac{1}{4}(1 – \xi)(1 – \eta)$ $N_{2} = \frac{1}{4}(1 + \xi)(1 – \eta)$ $N_{3} = \frac{1}{4}(1 + \xi)(1 + \eta)$ $N_{4} = \frac{1}{4}(1 – \xi)(1 + \eta)$ The above shape functions are in fact the Lagrangian interpolation Note that we define the element as a square of size … Read more

Strong formulation (or Strong form): the partial differential equation that governs the problem. For example: the equilibrium equation in solid mechanics, the Fourier’s equation for transport of thermal energy, the Fick’s law for mass transport, etc. Below is the equilibrium equation in solid mechanics, which satisfies at every point of the problem domain. $\nabla \cdot … Read more