Routing vehicle problem

by

The Routing vehicle problem (RVP) can be considered as a generalization of the Traveling salesperson problem (TSP). It short, the objective is to find the optimal routes for multiple vehicles to visit a set of locations. The objective is to minimize the total cost of multiple trucks (the number of trucks is known beforehand and does not change). Each truck must start from the depot to travel through some certain stores and return to the depot. Assume that the route between any two locations (either depot or stores) is simply the linear distance. The capacity of each truck and the demand of each store are known. Each store is only visited by one truck and each truck is not allowed to visit any store more than once. The truck is also not permitted to be overloaded.

It is straightforward to solve RVP based on the solution TSP, with consideration of 2 following modifications:

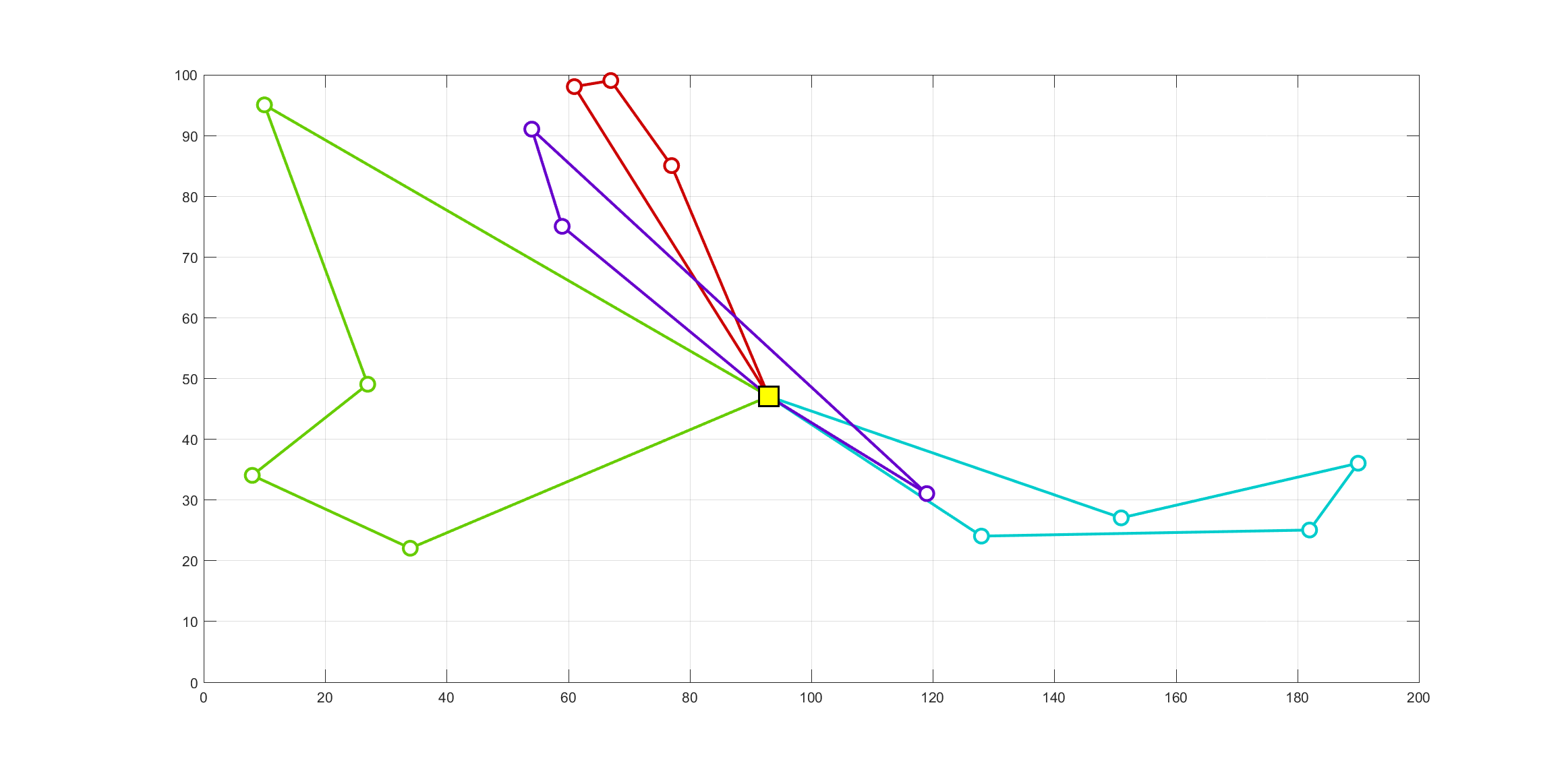
  1. Insert extra pseudo depots into the solution. The number of pseudo depots is equal to the number of trucks minus one. For example, assume that we have 14 stores and 4 trucks. We can denote 0 for the depot, and number 1 to 14 for the stores. Because there are 4 trucks, 3 pseudo depots are needed and they are denoted by the number 15, 16, and 17. If a solution is as follows: 1 2 5 4 9 7 15 6 13 16 8 12 3 11 17 10 14, it means that the four routes are: (0) 1 2 5 4 9 7 (0), (0) 6 13 (0), (0) 8 12 3 11 (0), (0) 10 14 (0). It is then easy to calculate the cost (e.g. distance) of each route.
  2. Define a penalty term. The penalty term is necessary to mark the infeasible solution, where any of the four trucks is overloaded. The more trucks are overloaded, the higher value of penalty term is.

Figure 1 presents an illustration of RVP with 14 stores and 4 trucks.

Figure 1. Illustration of a Routing Vehicle Problem

Possible extensions would be:

  • Multiple depots: there exists more than one depot, each depot can only serve a limited number of trucks. For example, we have 5 trucks and 2 depots. One depot can serve 2 trucks, the other can serve 3 trucks
  • Multiple commodities: some types of commodities cannot be transported together, each store can only accept some certain types of commodities.
  • etc.