Parameter identification is usually encountered in engineering. Some types of problems are listed below.
Curve fitting. This is a simple problem when we only have to find the relation between two sets of data: $x$ and $y$. The most common example would be “linear regression”, such that we assume a linear relation: $y = ax + b$. The parameters to be identified are $a$ and $b$.
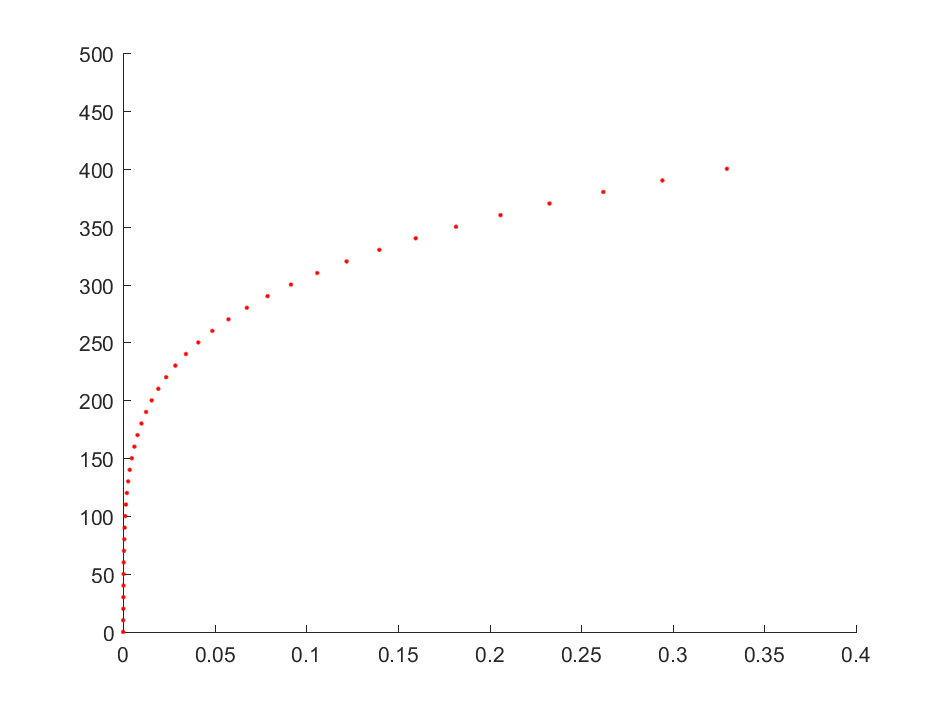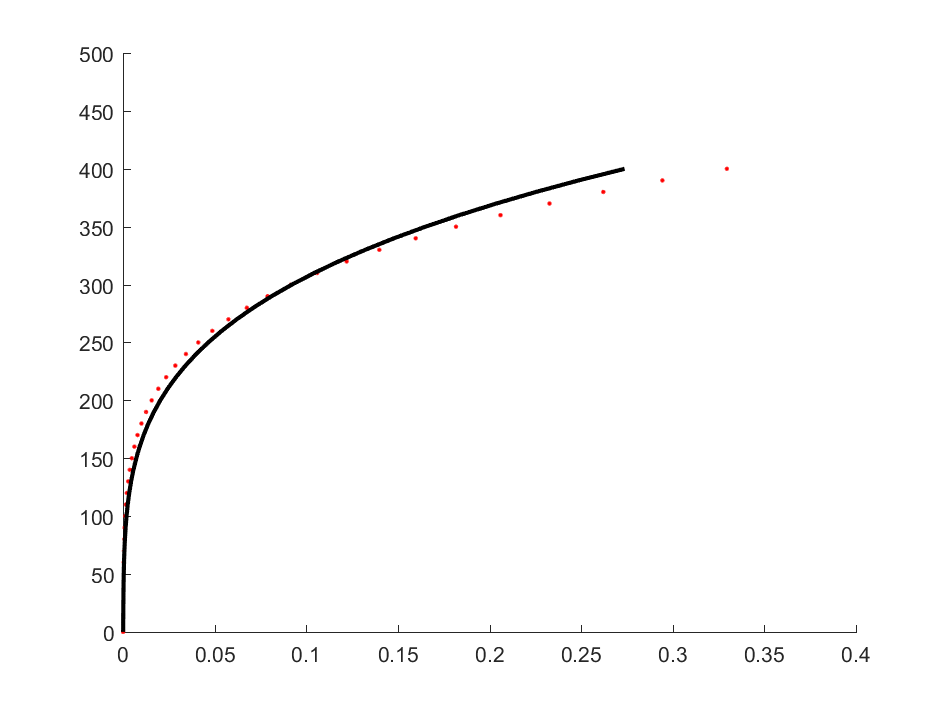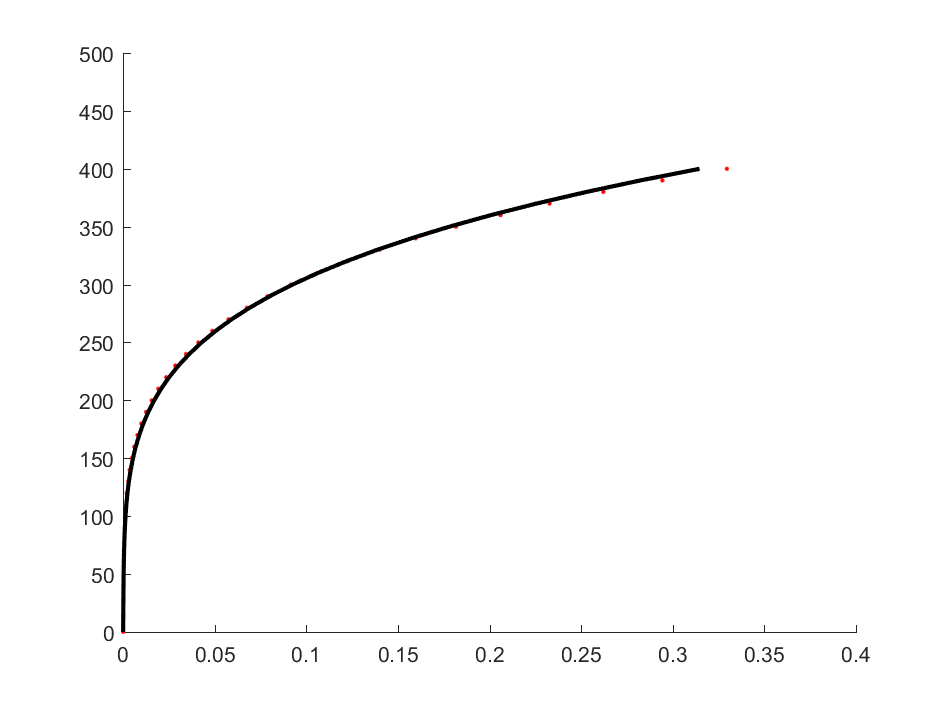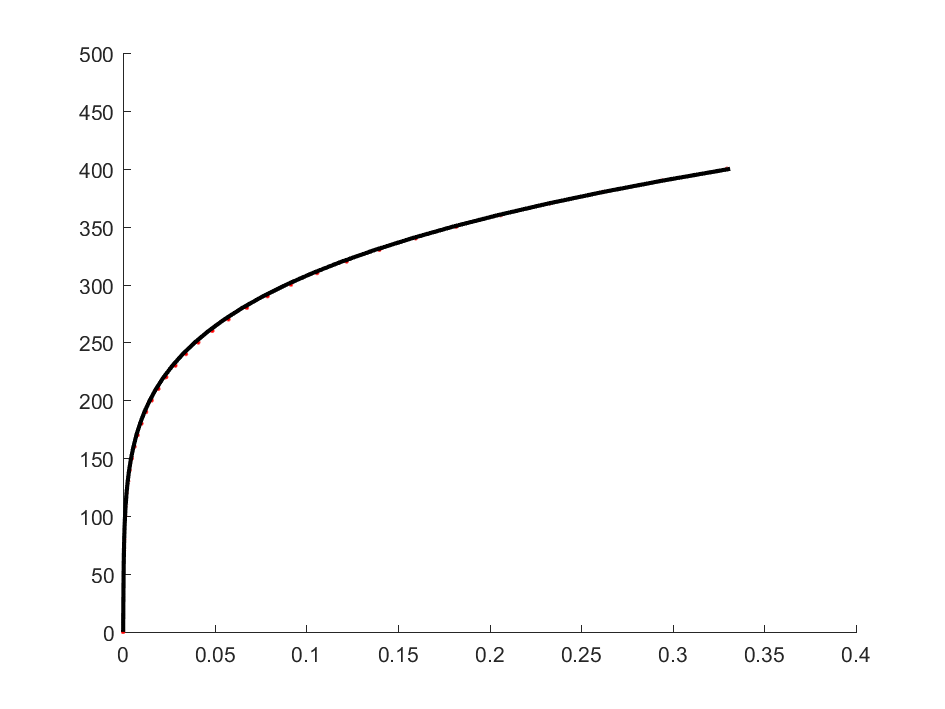
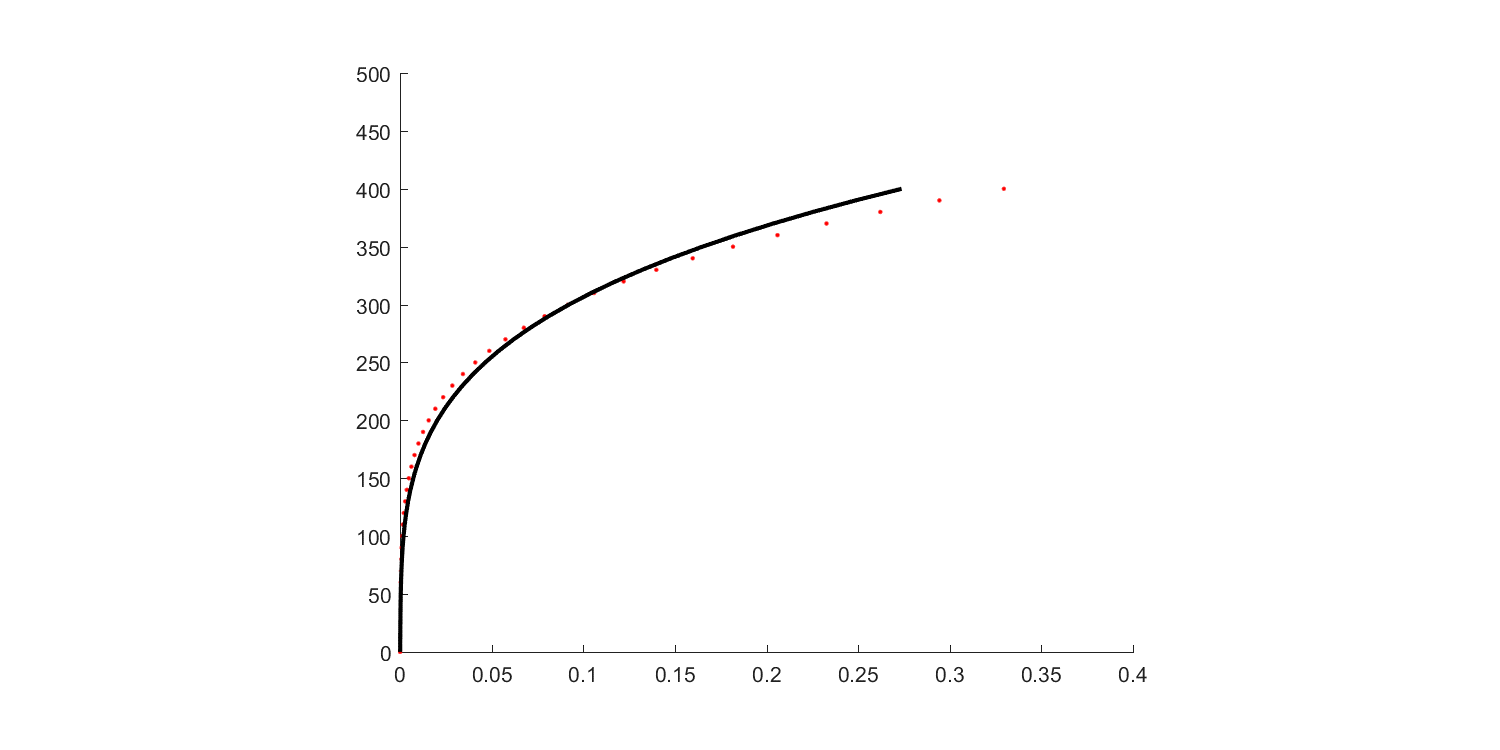
For example, we have the data for stress ($\sigma$) and strain ($\varepsilon$). Taking the horizontal axis as strain and the vertical axis as stress, the data points are depicted as red dots in Figure 1. Assume that the stress-strain relation satisfies the following equation $ \varepsilon = \frac{\sigma}{E} + (\frac{\sigma}{K})^{1/n}$ (Ramberg – Osgood model). The three parameters to be identified are: $E$, $K$ and $n$.
Material parameters identification. Basically, a material constitutive law involves various parameters. Not all of them can be easily and/or directly measured. Instead, such material parameters are identified via experiments. That is, the set of unknown material parameters has to be determined such that it leads to results close to experimental data. For example: identification of parameters for the yield criterion in metal forming (Hill criterion, Barlat criterion, etc.), identification of parameters for hyper-elastic material (Mooney-Rivlin model, Ogden model, etc.)
Damage parameters identification. This problem is encountered in Structural Health Monitoring in which the following questions have to be answered: Where is the damage located? How severe is the damage? (the severity can be assessed by the reduction in structural stiffness, with reference to a “standard condition”).A parameter identification problem can be solved as follows. Firstly, an assumption must be made, that the experimental data can be described by a chosen material model. This step would require experience and expertise. Secondly, a numerical model to simulate the experiment should be developed. For instance, if we have the load-displacement curve from uni-axial tensile test data, it is essential that we can get load-displacement curve from numerical simulation. The accuracy of the numerical model is important. Therefore, it must be verified and validated. Thirdly, an optimization is stated, in which the objective function is the error between experimental data and the results obtained from simulation. Design variables are the parameters to be identified. Constraints may also apply, depending on the specified problem.
