Let us consider an elastic deformable body $\Omega$. The discrete form of equilibrium equation should take the following form
$\mathbf{K} \mathbf{u} = \mathbf{F}$,
where $\mathbf{K}$ is the stiffness matrix, $\mathbf{F}$ is the vector of (external) load, and $\mathbf{u}$ is the vector of nodal displacements.
For simplicity, we assume that $\Omega$ is a two dimensional rectangular domain, and has been discretized by $4 \times 3$ elements as n Figure 1.

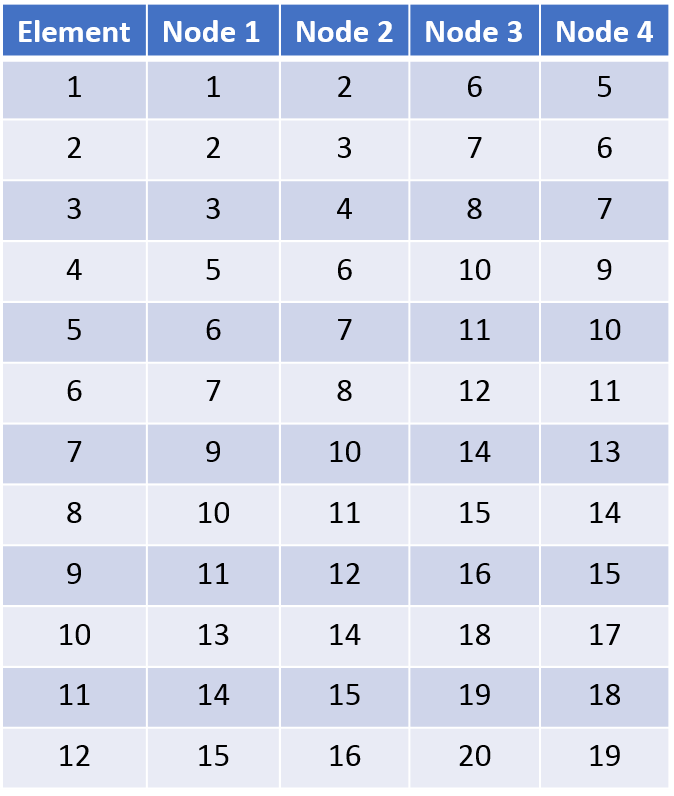
The matrix of connectivity (the matrix that shows which nodes belong to which element) is presented in Figure 2
For each node, there are two degrees of freedom (dofs), which are the horizontal and vertical components of displacements. The numbering for dofs is taken as follows. Node 1: dof 1 (horizontal displacement) and dof 2 (vertical displacement). Node 2: dof 3 and dof 4. Node $I$: dof $2I-1$ and dof $2I$
Element 1 has four nodes: 1, 2, 6, and 5 (global index, see Figure 2 and Figure 1). Following the numbering of dofs as mentioned above, we can write the vector of dof indices (elemdof) for element 1 as follows (Figure 3)

The vector of dof IDs help us to assemble the matrix. Here we have totally 20 nodes, and each node has 2 dofs, hence the size of global stiffness matrix is $40 \times 40$. For a four-node quadrilateral element, the element stiffness matrix has the size $8 \times 8$. If we denote $i, j$ as the row index and column index of the element matrix, and $I, J$ the corresponding row index and column index of the global matrix. We have the following relation
$I = elemdof(e, i)$, and $J = elemdof(e, j)$,
in which $e$ is the index of element.
In short, the value at row $i$, column $j$ of an element matrix should be added to the value at row $I$, column $J$ of the global matrix. For example, the value at row 2, column 5 of the element stiffness matrix of element 1 will be added to the position at row 2, column 11 of the global stiffness matrix.