Strong formulation (or Strong form): the partial differential equation that governs the problem. For example: the equilibrium equation in solid mechanics, the Fourier’s equation for transport of thermal energy, the Fick’s law for mass transport, etc. Below is the equilibrium equation in solid mechanics, which satisfies at every point of the problem domain.
$\nabla \cdot \boldsymbol{\sigma} + \rho \mathbf{b} = \rho \ddot{u}$,
where $\boldsymbol{\sigma}$ is the stress tensor; $\rho$ is the mass density; $\mathbf{b}$ is the body force and $\ddot{u}$ is the second order derivative of displacement $u$ (also known as acceleration).
Weak formulation (or weak form). The weak form is obtained from the strong form, by using Galerkin method. Hence, it is also referred to as the Galerkin weak form. In fact, the partial differential equation is converted in to an equation with integral terms, e.g. for linear elasticity
$\int \limits _{\Omega} \delta u \cdot (\rho \ddot{u}) $ d$\Omega$ + $\int \limits _{\Omega} \delta \boldsymbol{\varepsilon} : \boldsymbol{\sigma}$ d$\Omega = \int \limits _{\Gamma_{2}} \delta u \cdot \bar{q}$ d$\Gamma$ $+ \int \limits _{\Omega} \delta u \cdot (\rho \mathbf{b})$ d$\Omega$.
Here, $\delta u$ is the test function of displacement (please connect with the virtual displacement and the principle of virtual works in mechanics); $\boldsymbol{\varepsilon}$ is the strain tensor; $\bar{q}$ is the surface traction. The weak form enables the application of “divide and conquer” idea, that is transforming of a continuous problem into a discrete problem.
Meshing: the task that divides the problem domain into non-overlapping sub-domains.
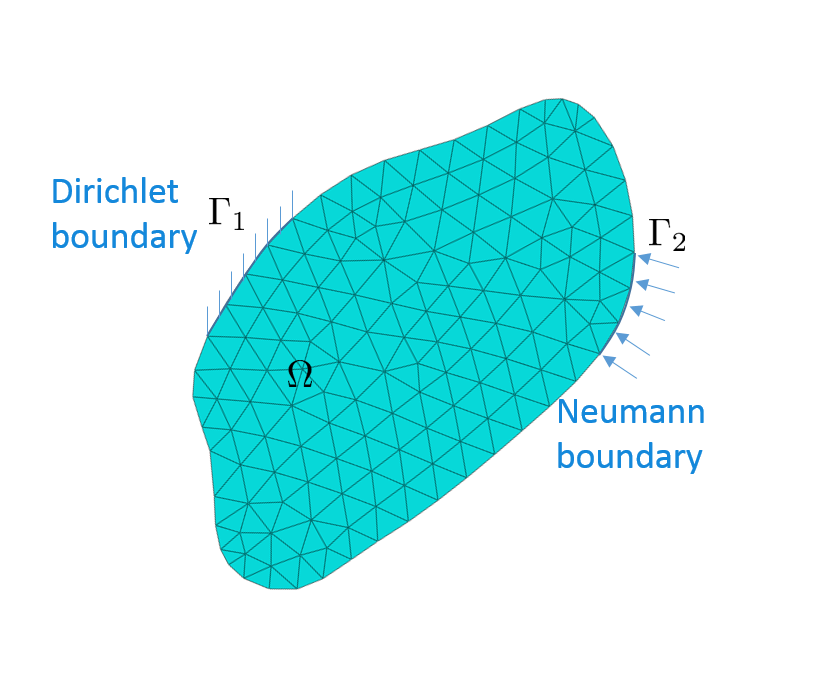
Element: each sub-domain is called an element. For convenience (in mathematical computation), an element often takes simple geometric shape, such as triangle or quadrilateral in 2D problems. In 3D problems, an element can have the shape of tetrahedron and hexahedron.
Node: the nodes are the vertices of elements.
Degrees of freedom (DOFs): the DOF(s) are defined at nodes and are the unknowns to be determined of the problem. The number and physical meaning of DOFs depends on type of problem. For example, in 2D linear elasticity, each node is associated with 2 DOFs, which represent the vertical and horizontal component of displacement field. In other words, the unknowns to be found are the nodal values of vertical and horizontal displacement.