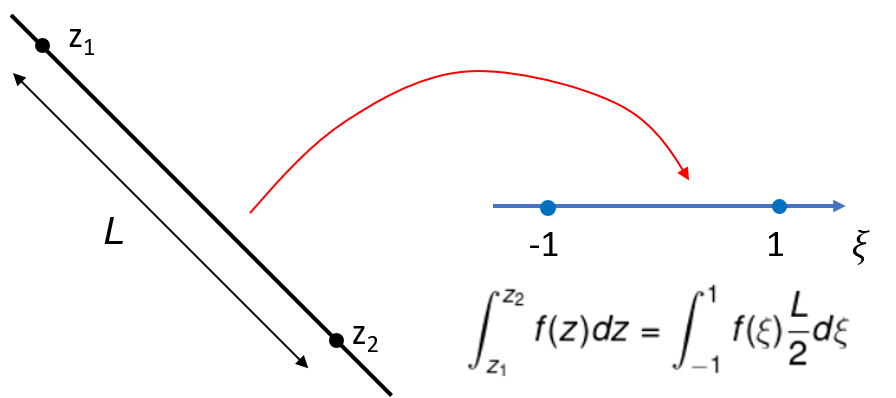
Integration on any straight line of length $L$ can be transformed into integration on the interval [-1, 1] by a simple transformation
$\int_{z_{1}}^{z_{2}} f(z) dz = \int \limits_{-1}^{1} \frac{L}{2} f(\xi) d\xi$
Note that the equation for transformation reads
$z = \frac{z_2 – z_1}{2} \xi + \frac{z_1 + z_2}{2}$
The integration on interval [-1,1] can be approximated by a summation.
$\int \limits_{-1}^{1} f(\xi) d\xi \approx \sum \limits_{i=1}^{n} w_{i} f(\xi_i)$
The above equation is the common form for numerical evaluation of integration. Following the Gaussian quadrature, the coordinates and weights of n integration points (or Gauss points) can be referred to 